κεφάλαιο 15
παραγοντοποίηση φυσικών αριθμών









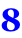












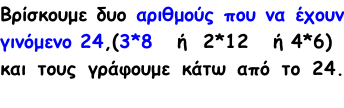
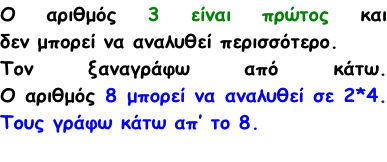


Και τι αποτέλεσμα θα είχαμε αν στην αρχή δεν διαλέγαμε το 3*8 αλλά το 2*12 ή το 4*6 ;
Ακριβώς το ίδιο.






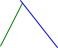
















Ας πάρουμε τον αριθμό 60. Τον γράφουμε και τραβάμε μια κάθετη γραμμή στα δεξιά του.
Εξετάζουμε ποιος είναι ο μικρότερος πρώτος αριθμός που διαιρεί ακριβώς το 60. Είναι το 2. Διαιρούμε το 60 με το 2 και γράφουμε κάτω από το 60 το πηλίκο της διαίρεσης δηλαδή το 30. (το πηλίκο της διαίρεσης 60:2) .
Συνεχίζουμε την ίδια διαδικασία για το 30. Διαιρούμε με το 2 , γιατί είναι ο μικρότερος πρώτος αριθμός που το διαιρεί , και γράφουμε το πηλίκο της διαίρεσης που είναι το 15. (30:2).
Το 15 δε διαιρείται με το 2. Πάμε στον επόμενο πρώτο αριθμό που είναι το 3 και εξετάζουμε αν διαιρείται με το 15. Διαιρούμε με το 3 και γράφουμε το πηλίκο της διαίρεσης που είναι το 5.
Το ίδιο κάνουμε και για το 5, που το διαιρούμε με το 5 , και καταλήγουμε σε πηλίκο 1. Τότε τελειώνει και η ανάλυση.
Άρα ο αριθμός 60 εκφράζεται ως γινόμενο πρώτων παραγόντων ως εξής:
60 = 2 Χ 2 Χ 3 Χ 5











Β. με διαδοχικές διαιρέσεις
Στις διαδοχικές διαιρέσεις , όπως και στα δεντροδιαγράμματα ,
δε με ενδιαφέρει η σειρά των πρώτων αριθμών
με την οποία διαιρώ τον σύνθετο και τα πηλίκα που προκύπτουν.
Με όποιον τρόπο και αν γίνει αυτό, το γινόμενο των πρώτων αριθμών είναι το ίδιο.

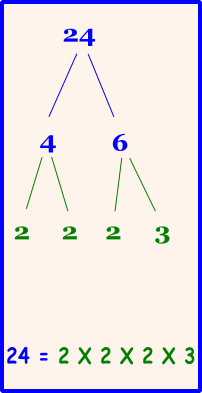
Η ανάλυση τελειώνει, όταν όλοι οι παράγοντες
είναι πρώτοι αριθμοί όπως εδώ (3,2, 2 και 2).
Άρα ο αριθμός 24 μπορεί να εκφραστεί
ως γινόμενο πρώτων παραγόντων ως εξής:
24 = 3 Χ 2 Χ 2 Χ 2
ΠΑΡΑΓΟΝΤΟΠΟΙΗΣΗ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ
Ένας σύνθετος αριθμός μπορεί να εκφραστεί και ως γινόμενο πρώτων αριθμών (γινόμενο πρώτων παραγόντων).
Π.χ. 24= 2*2*2*3 60=2*2*3*5
Μπορούμε να αναλύσουμε ένα σύνθετο αριθμό σε γινόμενο πρώτων παραγόντων με δύο τρόπους:
Α. με δεντροδιαγράμματα
Β. με διαδοχικές διαιρέσεις

Εξάσκηση - QUIZ & Παιχνίδια
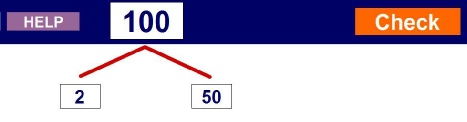
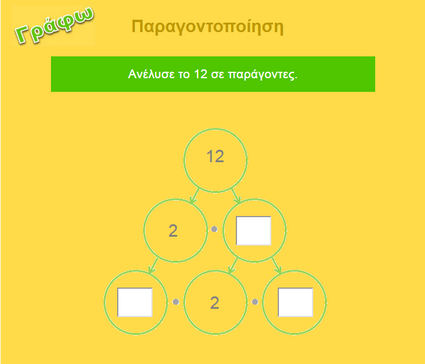
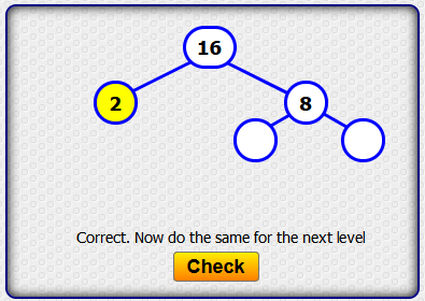
Στην επόμενη οθόνη γράφεις μέσα στα κουτάκια την ανάλυση του αριθμού που βλέπεις στην κορυφή και πατάς  . Συνεχίζεις μέχρι την ολοκλήρωση της ανάλυσης.
. Συνεχίζεις μέχρι την ολοκλήρωση της ανάλυσης.

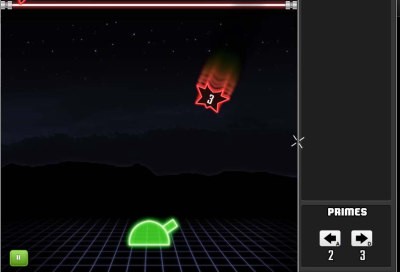
Πυροβόλησε τους αριθμούς με το κανόνι.
Με το ποντίκι σημαδεύεις τους αριθμούς και με τα βελάκια του πληκτρολογίου (δεξιό και αριστερό) ρίχνεις τους πρώτους αριθμούς που φαίνονται κάτω δεξιά στην οθόνη σου.
Πρέπει να πυροβολείς κάθε αριθμό με έναν διαιρέτη του , ώσπου να γίνει 1. Π.χ. Τον αριθμό 25 τον πυροβολείς με το 5 και γίνεται 5 (25:5) , ύστερα ξανά με το 5 και γίνεται 1 (5:5).
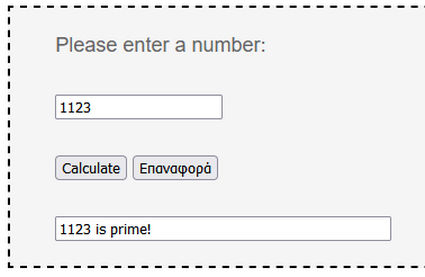
Αριθμομηχανή πρώτων αριθμών. Γράψε οποιονδήποτε αριθμό και πάτησε το Calculate ώστε να δεις αν είναι πρώτος (Prime) ή όχι.
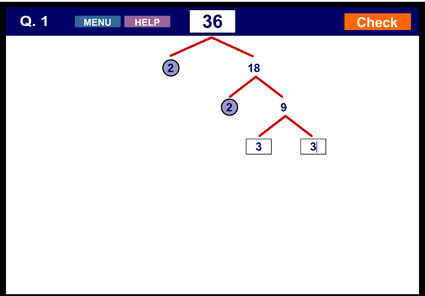
Ανάλυση αριθμών σε γινόμενο πρώτων παραγόντων.
Κόψε τους σύνθετους αριθμούς με το σπαθί σου μέχρι να γίνουν γινόμενο πρώτων παραγόντων.
Ανάλυση αριθμών σε γινόμενο πρώτων παραγόντων.


Μηχανή εύρεσης των διαιρετών (factors) και των πρώτων παραγόντων (prime factors) ενός αριθμού.























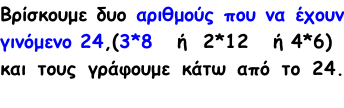
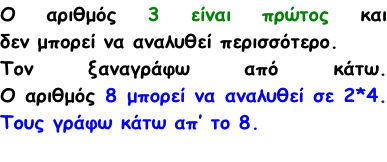





























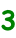




















 . Συνεχίζεις μέχρι την ολοκλήρωση της ανάλυσης.
. Συνεχίζεις μέχρι την ολοκλήρωση της ανάλυσης.