|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
2 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
30 |
32 |
34 |
36 |
38 |
40 |
|
3 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
33 |
36 |
39 |
42 |
45 |
48 |
51 |
54 |
57 |
60 |
|
4 |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
64 |
68 |
72 |
76 |
80 |
|
5 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
100 |
|
6 |
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
60 |
66 |
72 |
78 |
84 |
90 |
96 |
102 |
108 |
114 |
120 |
|
7 |
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
70 |
77 |
84 |
91 |
98 |
105 |
112 |
119 |
126 |
133 |
140 |
|
8 |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
80 |
88 |
96 |
104 |
112 |
120 |
128 |
136 |
144 |
152 |
160 |
|
9 |
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
90 |
99 |
108 |
117 |
126 |
135 |
144 |
153 |
162 |
171 |
180 |
|
10 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
150 |
160 |
170 |
180 |
190 |
200 |
|
11 |
11 |
22 |
33 |
44 |
55 |
66 |
77 |
88 |
99 |
110 |
121 |
132 |
143 |
154 |
165 |
176 |
187 |
198 |
209 |
220 |
|
12 |
12 |
24 |
36 |
48 |
60 |
72 |
84 |
96 |
108 |
120 |
132 |
144 |
156 |
168 |
180 |
192 |
204 |
216 |
228 |
240 |
|
13 |
13 |
26 |
39 |
52 |
65 |
78 |
91 |
104 |
117 |
130 |
143 |
156 |
169 |
182 |
195 |
208 |
221 |
234 |
247 |
260 |
|
14 |
14 |
28 |
42 |
56 |
70 |
84 |
98 |
112 |
126 |
140 |
154 |
168 |
182 |
196 |
210 |
224 |
238 |
252 |
266 |
280 |
|
15 |
15 |
30 |
45 |
60 |
75 |
90 |
105 |
120 |
135 |
150 |
165 |
180 |
195 |
210 |
225 |
240 |
255 |
270 |
285 |
300 |
|
16 |
16 |
32 |
48 |
64 |
80 |
96 |
112 |
128 |
144 |
160 |
176 |
192 |
208 |
224 |
240 |
256 |
272 |
288 |
304 |
320 |
|
17 |
17 |
34 |
51 |
68 |
85 |
102 |
119 |
136 |
153 |
170 |
187 |
204 |
221 |
238 |
255 |
272 |
289 |
306 |
323 |
340 |
|
18 |
18 |
36 |
54 |
72 |
90 |
108 |
126 |
144 |
162 |
180 |
198 |
216 |
234 |
252 |
270 |
288 |
306 |
324 |
342 |
360 |
|
19 |
19 |
38 |
57 |
76 |
95 |
114 |
133 |
152 |
171 |
190 |
209 |
228 |
247 |
266 |
285 |
304 |
323 |
342 |
361 |
380 |
|
20 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
220 |
240 |
260 |
280 |
300 |
320 |
340 |
360 |
380 |
400 |
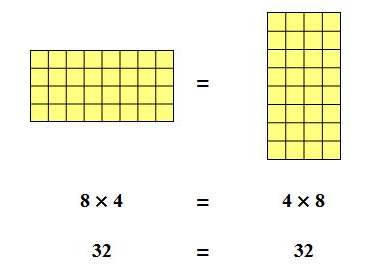























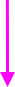






















































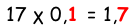






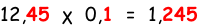





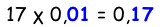





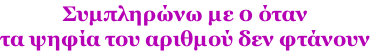






















| 45 Απεικονίζω δεδομένα με ραβδόγραμμα ή εικονόγραμμα |
| 46 Ταξινομώ δεδομένα - εξάγω συμπεράσματα |
| 47 Άλλοι τύποι γραφημάτων |
| 48 Βρίσκω το μέσο όρο |
| ΕΠΑΝΑΛΗΠΤΙΚΟ 4ης Ενότητας |
| 49 Μετρώ το μήκος |
| 50 Μετρώ και λογαριάζω βάρη |
| 51 Μετρώ το Χρόνο |
| 52 Μετρώ την αξία με χρήματα |
| 53 Γεωμετρικά μοτίβα |
| 54 Αριθμητικά μοτίβα |
| 55 Σύνθετα μοτίβα |
| ΕΠΑΝΑΛΗΠΤΙΚΟ 5ης Ενότητας |
 Ο
Ο